Energy Bands in Solids - Engineering Physics

Energy Bands in Solids 

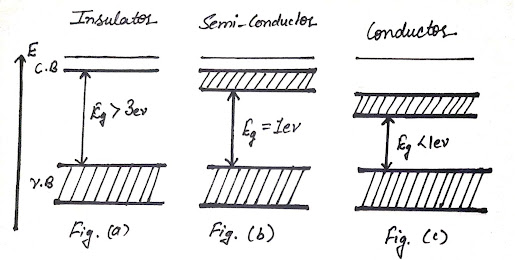
In the case of insulators, there is no effective force electron. All bands are completely full in the valence bands, and the conduction band is completely empty and there is large forbidden energy gapbetween these two bands as shown in Fig. (a) and it is impossible to excite an electron across this region. All the bands are either completely filled or empty at any temperature. So the external electric field can not produce any current. So the conductivity of such materials under ordinary conditions is zero and are called insulators. A representative example of an insulator is a diamond where two bands separated by an energy gap of.

When the forbidden gap is small, the order of 1eV or less as shown in Fig. (b), so that electrons could be excited thermally from states near the top of the filled band to a state near the bottom of the next empty band across the bandgap. Hence a limited number of electrons are available for conduction in the conduction band which is almost empty, on applying an electric field. The material of this type is called a semiconductor. At low temperature (0K) the valence band is completely empty. So a semiconductor virtually behaves as an insulator at low temperature. Even at room temperature some electrons cross the conduction and impart little conductivity to the semiconductor. As the temperature is increased, more and more electrons cross over to the conduction band, and the conductivity increases. Examples of semiconductors are Germanium (bandgap 0.67eV) and Silicon (bandgap 1.1eV).

The energy band structure in solids have two possibilities

1. A solid is a conductor if either its conduction band is not completely filled and the valence band may be completely filled and there is an extremely small energy gap between them as shown in Fig. (c) For example Li, Na, K, etc.

2. The valence band is completely filled and the empty conduction band overlap with the valence band (For example Ba, Cd, Zn, etc.) So the energy gap is zero. The electron in the valence band is free to move inside the crystal lattice. The electrons under the influence of a small applied field acquire additional energy and move to a higher energy state. These mobile electrons constitute a current.

For Kronig-Penney Model - Click Here 

For Direct and Indirect bandgap in semiconductor - Click Here