Bloch Theorem
The band theory of
solid assume that electron move in a periodic potential of the period ‘a’ (lattice
constant).
i.e
The Schrodinger's equation for free-electron moving in a constant potential V0 is
given as
So the Schrodinger's equation for an electron moving in periodic potential V(x) is written as
The solution of Eq. (3) are of the type
Where is known as Bloch function and which is again
periodic with the same periodicity of the lattice.
is known as Bloch function and which is again
periodic with the same periodicity of the lattice.
Where
Thus Bloch Theorem is a
mathematical statement regarding the form of the one-electron wave function for
a perfectly periodic potential.
Proof -
We know that
Schrodinger wave eq. (3) is a second-order differential eq. and hence there
exist only two real independent solutions for this equation.
Say f(x)
 ...(7)
...(7)Let![]() be another solution of eq. (3), hence it
must be represented as
be another solution of eq. (3), hence it
must be represented as
By using eq. (7) and
(8), above eq. become
Now, by using eq.
(6), we can write eq. (9) as
Now, by comparing eq.
(11) and (12), we get
Now eq. (13) have
non-vanishing solutions for A and B if and only if the determinant of the coefficient is zero, i.e.,
We have written in eq. (15) and this result is proved below
this topic.
in eq. (15) and this result is proved below
this topic.
Now, eq. (15) gives
two roots of ,
so there are two wave functions
,
so there are two wave functions and
and . It must be noted that
. It must be noted that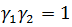 and
and is a real function of energy E.
is a real function of energy E.
Let us consider two
cases for the energy ranges.
In this case the two
roots will be the complex conjugate of each other, we can write and
and Where K is real and the
corresponding wave functions
Where K is real and the
corresponding wave functions and
and can be written as
can be written as
i.e., in general
Case 2. For energy range

In this case the roots are real and will be reciprocals of each other these correspond to wave functions of the type
AndWhere is real. These are not acceptable wave
functions since these are not
bounded and approaches
is real. These are not acceptable wave
functions since these are not
bounded and approaches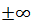 when approaches infinity. Thus we find that the energy spectrum of an electron in a periodic potential consists of allowed and
forbidden energy regions as bands. This will further be discussed in
Kroning-Penney Model.
when approaches infinity. Thus we find that the energy spectrum of an electron in a periodic potential consists of allowed and
forbidden energy regions as bands. This will further be discussed in
Kroning-Penney Model.
As f(x)
Multiply f
i.e the wronskian












































0 Comments
If you have any doubt, please let me know