Sommerfield‘s Quantum Theory of free electron - Engineering Physics

Sommerfield‘s Quantum Theory

In 1928, Sommerfield suggested that electron gas should be treated quantum mechanically in the light of Pauli's exclusion principle which states that no two particles can have all the quantum numbers identical. He used Fermi-Dirac statistics rather than Maxwell-Boltzmann statistics and succeeded in explaining many experimental facts. We first find the possible energy states in one-dimensional and then extend the idea to three-dimensional case.

Free Electron Gas in one-dimensional Box

Consider an electron having mass m confined to move in a one-dimensional rectangular box of length L i.e., The electron moves along a straight line say along the x-axis, let the wall of the box be rigid and non-penetrable. Let the electron can travel along the x-axis between x=0 and x= L.

The potential V is defined as

The Schrodinger’s wave equation for the wave-function of the electron moving along the x-axis in a straight line may be written as 

For free electron inside the box V=0, so the above eq. becomes

Where E is the Kinetic-energy of the electron

Or  

 ...(1)

Where 

 ...(2)
The general solution of Eq. (1) may be written as

 ...(3)

Where A and B are the constants to be determined by the boundary conditions.

Boundary condition

The wave function Ψ=0 at x=0 and x=L

1. At x=0, Ψ=0, so eq. (3) becomes

0= 0+B

B=0

So eq. (3) becomes

Ψ= A Sin Kx  …(4)

2. At x=L, Ψ=0, so eq. (4) becomes

 0 = A Sin Kx (A is constant so can't equal to 0  )

 ...(5)

For nth state eq. (4) becomes

 ...(6)

Using eq. (2), eq. (5) can be written as

Or 

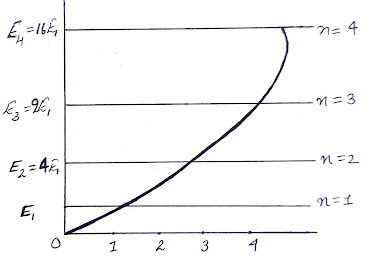
Since E depends on ‘n’, so let us denote the energy of the electron by E_n ...(7)

The number n is called the quantum number. We find the lowest energy is obtained when n=1

From eq. (7), we have 

i.e., 

 ...(8)

Now, the spacing between the energy levels can be found by

The Energy level diagram is shown as - 

That’s mean energy level separation increases with n.

Fermi Energy

At T=0K, there will be no thermal excitation i.e., all the electrons remain at ground level. For a large value of n, there will be the uppermost filled level at T=0K called the Fermi level. This is the last filled level. The energy of the Fermi level is called Fermi Energy.

…(9)

In a linear solid, there are two quantum numbers of a conduction electron orbital i.e., n (=1,2,3…) and spin s (1/2). This means that for each value of n,s can have two values depending upon the orientation of the electron. Electrons are indistinguishable particles and obey Pauli’s exclusion principle states that no two electrons can have all four quantum numbers identical. Hence every orbital or quantum state n can accommodate two electrons one with spin up and the other with spin down. In other words, each energy level is doubly degenerate.

Let n_F denotes the uppermost filled energy level, and if there are N electrons we can write

Hence eq. (9) give

 …(10)                     

This is the Fermi energy in 1-Dim.

Total Energy or Ground state Energy –

At T=0K, all the electrons are in ground state i.e., there is no thermal excitation. Sum of all the energy states will be total ground state energy.

Here factor 2 comes into the picture, since each level accommodates two-electron with equal energies.

Above eq. can be written as

  …(11)

As we know 

In a solid, total no. of electrons are very large, suppose S=1000, then we can neglectand  S as compare to

                                                           

So 

  ….(12)

Thus, we find that for one-dimension, the average energy in the ground state is one-third of that of the Fermi energy.

Some Important formulae for Numerical problem-

From eq. (5), eq. (10) can be written as

If the electron is free then its whole energy will be Kinetic energy 

i.e.,

where  

Where 

Now, Fermi velocity, 

And Fermi Temperature, 

Where 

For Classical theory of free electron - click here 

For Density of State in 1-D, 2D and 3D - Click here