Introduction
Free Electron means unbound electron of the atom of any metal
which can move freely. Many properties of metal-like electrical conductivity,
magnetic susceptibility, Thermal conductivity, Mechanical strength,
optoelectronic properties, etc. depend on the free electrons.
Free electron theory are of two types-
1. Classical or Drude-Lorentz Theory
2. Quantum or Sommerfield Theory
This theory was first proposed by Lorentz and Drude with the
help of classical laws of physics. The classical theory of free electron explains
the properties like ohm’s law, metallic luster, etc. but it could not explain heat
capacity and the paramagnetic susceptibility of the conduction electrons. The
Quantum theory removed the limitations of classical theory by using statistics
developed by Sommerfield and succeeded in explaining many experimental facts.
Drude-Lorentz or Classical Theory
In 1909, Lorentz suggested that this free electron gas
behaves like perfect gas obeys Maxwell-Boltzmann statistics. Hence, the
classical theory is also known as the Drude-Lorentz theory.
Success of Free
Electron Theory
The free-electron theory successfully explained
1. Electrical conductivity
2. Ohm’s Law
3. Thermal conductivity
4. Weidmann-Franz law
5. Complete opacity of metals and their high luster
1. Electrical
conductivity
It is defined as the amount of electricity that flows in unit
time per unit area of cross-section of the conductor per unit potential
gradient.
If λ is the mean free path of electrons, then the relaxation time τ between two successive collisions is given by
If q charge is flowing through a conductor of cross-section area A in time t, then
Or,
For the unit area of cross-section
This expression show
that conductivities of different materials depending on the number of free
electron, T, and A.
2. Ohm’s law
From eq. (1.6) we have
This is microscopic
form of ohm’s law.
3. Thermal conductivity
There is no transfer of
energy, if there is no temperature difference between two points in a system.
So to discuss the thermal conductivity of metals, we suppose that a temperature
gradient exists across the system instead of the voltage gradient, hence the
transport of thermal energy takes place due to this gradient.
Suppose A and B be the
two ends of the system in the form of a metallic rod and end A is at a higher
temperature than B, then the thermal conductivity from A to B takes place by
electrons. In a collision, the electron near A loose their kinetic energy while
the electrons near B gain energy.
The amount of heat Q passing through a cross-section of the rod per unit area per second is given by
Where λ is mean free path, v
is the velocity of electrons and n is the number density of free electron.
From Kinetic theory of gas
Hence Or This value of K is verified experimentally and the theory of the free electron is found to be successful to explain thermal conductivity.
4. Wiedemann-Franz
relation
In 1853, Weidmann and
Franz discovered that all good electrical conductors are also good thermal
conductors and the ratio of thermal conductivity to the electrical conductivity
at any temperature is constant for all metals.
i.e.,
using eqns. (1.7) and (1.10), we getThis is Weidmann-Franz
relation.
5. Lustre and opacity
of metals
When electromagnetic
radiations fall on metal, it produces forced oscillations in the free
electrons having the same velocity as that of electromagnetic radiations. Thus
the energy of incident radiations is absorbed by free electrons and the metal
appears opaque. The excited electron on returning to its initial state emits a photon having the same energy as is absorbed initially. This energy is given
out in the form of visible light in all directions, but only the light rays
directed towards the metal surface can get through. Hence, the metal appears to
reflect virtually all the light that is incident on it, giving it the
characteristic metallic luster.
Failure of the theory
1. It fails to explain the heat capacity of materials. According to this theory
But experimentally, 2. It does not explain the paramagnetic susceptibility of the conduction electrons, Experimentally χ is independent of T, but by this theory3. It does not explain why some
crystals are metallic.
4. It is unable to explain why
metals prefer certain structures.
5. It does not explain the temperature variation
of electrical resistivity because this theory predicts the variation of
resistivity as ![]() which actually is linear.
which actually is linear.
6. it is unable to differentiate insulator, semiconductor and conductor.
For Sommerfield's Quantum Theory of Free Electron - Click Here



























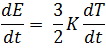














3 Comments
👍
ReplyDelete👍👍👍
DeleteNic
ReplyDeleteIf you have any doubt, please let me know